【第二種電気工事士】問2でよく出る「電気抵抗と抵抗率」をやさしく解説！

第二種電気工事士の筆記試験・問2では「抵抗率を求める問題」がよく出題されます。
一見むずかしそうに見えますが、公式と単位の意味を正しく理解しておけば、確実に得点できる問題です。

この記事では、「電気抵抗とは？」「抵抗率って何？」「材料によってどう変わるの？」という基本から、抵抗率の求め方や頻出の計算パターンまで、やさしく解説していきます。

電気が苦手な人でも理解できるように、図解や例題もまじえて紹介していくので、ぜひ最後まで読んでみてください！

この記事を書いている人

電気抵抗とは？｜電気の流れにくさを表す値

電気抵抗とは、電気の流れにくさを数値で表したものです。

たとえば、水がホースを通って流れる様子を思い浮かべてください。ホースの途中が細くなっていると、水が流れにくくなりますよね？
電気もそれと同じで、導線などの中を電流が流れるとき、内部の「通りにくさ」があるとスムーズに流れなくなります。

この流れにくさ＝抵抗を表すのが、電気抵抗（記号：R）です。

電気抵抗の単位は、オーム（Ω）です。

たとえば、同じ電池（電圧）を使っても、電気抵抗が大きな部品には電流がほとんど流れません。逆に、電気抵抗が小さな導線には多くの電流が流れます。

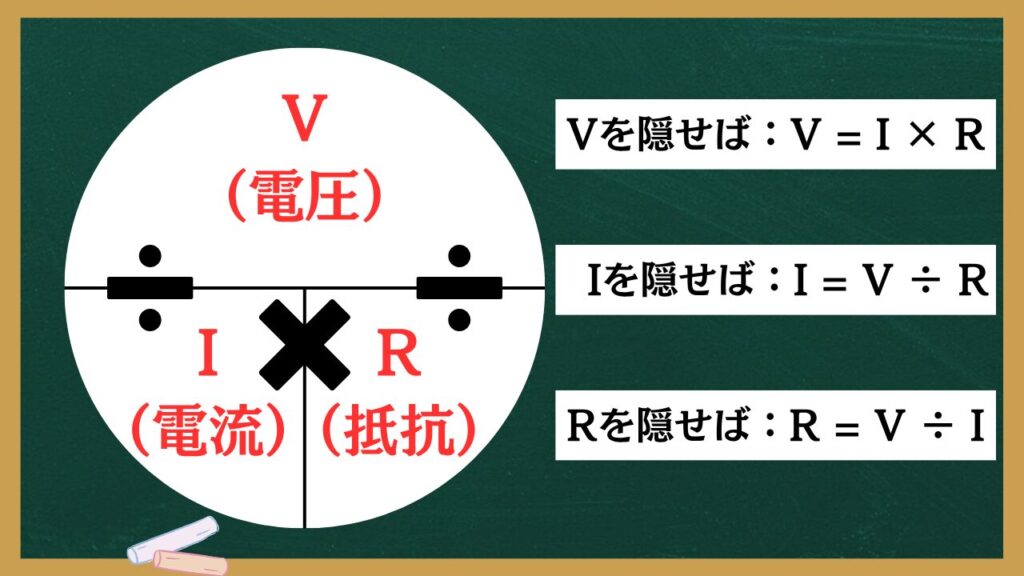
電気抵抗と電流・電圧の関係は、オームの法則で簡単に表せます。

V = R × I　（電圧＝抵抗×電流）

この式からもわかるとおり、抵抗が大きければ、同じ電圧でも電流は少なくなるのです。

オームの法則は、電気の話をするときに必要になる考えです。
まだマスターしていない人は、こちらの記事も参考にしてみてください
➡オームの法則で電流を求める基本計算｜第二種電気工事士の得点源をマスターしよう！

電気抵抗が「電流の流れにくさ」を表すのに対して、**抵抗率（導体の材質によって決まる性質）**は、「どんな金属が電気を流しやすいか・流しにくいか」を示す指標です。

たとえば、銅やアルミは電気をよく通すので、抵抗率が小さく、逆にゴムやプラスチックなどは電気をほとんど通さないので、抵抗率が非常に大きくなります。

電気抵抗値の公式は$$R＝ ρ\frac{ℓ}{A} $$

で表せます。

イメージで理解しよう！

令和7年度第二種電気工事士上期学科試験よりジュール熱の問題を抜粋

電気抵抗公式：$R＝ ρ\frac{ℓ}{A} $

問題文より、同じ材質で抵抗率が同一であるためρが消える

抵抗が等しくなるので

$ \frac{ℓ_1}{A_1} $＝$ \frac{ℓ_2}{A_2} $　➡　A₂＝A₁$ \frac{ℓ_2}{ℓ_1} $

ここで断面積$A = \frac{\pi d^{2}}{4}$

$\frac{\pi d_2^{2}}{4}$=$\frac{\pi d_1^{2}}{4}$×$ \frac{ℓ_2}{ℓ_1} $

ｄ₂＝ｄ₁×$\sqrt{\frac{\ell_2}{\ell_1}}$

ｄ₂＝1.6×$\sqrt{\frac{32}{8}}$＝1.6×$\sqrt{4}$＝1.6×2＝3.2[㎡]

よって答え：3.2[㎡]　（ハ）

point

抵抗・抵抗率は暗記だけでなく、「なぜそうなるか」をイメージで理解すると得点源になります。